Uncertainty principle
From Wikipedia, the free encyclopedia.
In quantum physics, the Heisenberg uncertainty principle states that one cannot assign with full precision values for certain pairs of observable variables, including the position and momentum, of a single particle at the same time. It furthermore precisely quantifies the imprecision by providing a lower bound (greater than zero) for the product of the standard deviations of the measurements. The uncertainty principle is one of the cornerstones of quantum mechanics and was discovered by Werner Heisenberg in 1927.
It is sometimes called the Heisenberg indeterminacy principle (a name prefered by Niels Bohr).
Contents |
Understanding uncertainty
Consider an experiment in which a particle is prepared in a definite state and two successive measurements are performed on the particle. The first one measures the particle's position and the second immediately after measures its momentum. Each time the experiment is performed, some value x is obtained for position and some value p is obtained for momentum. These values, however, may be different for each trial. In other words, there is an uncertainty in the outcome of the measurements. The Heisenberg uncertainty principle provides a quantitative relationship between the uncertainties of p and x as measured by their standard deviations in the following way: If the particle state is such that the first measurement yields a dispersion of values Δx, then the second measurement will have a distribution of values whose dispersion Δp is at least inversely proportional to Δx. This can be stated precisely by:
where 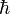 is Planck's constant (h) divided by 2π.
is Planck's constant (h) divided by 2π.
Wave analogy
There is a precise, quantitative analogy between the Heisenberg uncertainty relations and properties of waves or signals. Consider a time-varying signal such as a sound wave. It is meaningless to ask about the frequency spectrum of the signal at a moment in time. In order to determine the frequencies accurately, the signal needs to be sampled for a finite (non zero) time. This necessarily means that time precision is lost. In other words, a sound cannot have both a precise time, as in a short pulse, and a precise frequency, as in a continuous pure tone. The time and frequency of a wave in time are analogous to the position and momentum of a particle in space.
Overview
An uncertainty relation arises between any two observable quantities that can be defined by non-commuting operators. The uncertainty principle in quantum mechanics is sometimes explained by claiming that the measurement of position necessarily disturbs a particle's momentum. Heisenberg himself may have offered explanations which suggest this view, at least initially. That disturbance plays no role in the uncertainty principle can be seen as follows: Consider a particle prepared in a definite state, and measure either the momentum or the position of the particle, but not both. After repeating this experiment a large number of times, we will obtain probability distributions of values for both these quantities and the uncertainty relation still holds for the dispersions Δp, Δx of the values.
The Heisenberg uncertainty relations are a theoretical bound over all measurements. They hold for so-called ideal measurements, sometimes called von Neumann measurements. They hold even more so for non-ideal or Landau measurements.
Correspondingly, any one particle cannot be described simultaneously as a "classic point particle" and as a wave. The fact that either one of these descriptions is appropriate at least in separate cases is called wave-particle duality; a change of appropriate descriptions according to measured values is known as wavefunction collapse.) The uncertainty principle, as initially considered by Heisenberg, is concerned with cases in which neither of these two descriptions is fully and exclusively appropriate, such as a particle in a box with a particular energy value; i.e. systems which are characterized neither by one unique "position" (one particular value of distance from a potential wall) nor by one unique value of momentum (incl. its direction).
Formulation
If several identical copies of a system in a given state are prepared, measurements of position and momentum will conform to a determined probability distributions. This is a fundamental postulate of quantum mechanics. If we compute the standard deviation Δx of the position measurements and the standard deviation Δp of the momentum measurements, then
where 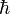 is Planck's constant (h) divided by 2π. (In some treatments, the "uncertainty" of a variable is taken to be the smallest width of a range which contains 50% of the values, which, in the case of normally distributed variables, leads to a larger lower bound of h/2π for the product of the uncertainties.) Note that this inequality allows for several possibilities: the state could be such that x can be measured with high precision, but then p will only approximately be known, or conversely p could be sharply defined while x cannot be precisely determined. In yet other states, both x and p can be measured with "reasonable" (but not arbitrarily high) precision.
is Planck's constant (h) divided by 2π. (In some treatments, the "uncertainty" of a variable is taken to be the smallest width of a range which contains 50% of the values, which, in the case of normally distributed variables, leads to a larger lower bound of h/2π for the product of the uncertainties.) Note that this inequality allows for several possibilities: the state could be such that x can be measured with high precision, but then p will only approximately be known, or conversely p could be sharply defined while x cannot be precisely determined. In yet other states, both x and p can be measured with "reasonable" (but not arbitrarily high) precision.
In everyday life, we do not usually observe these uncertainties because the value of Planck's constant (h) is extremely small.
Other characterizations
A number of additional characterizations have been developed including the ones below.
Generalized applications
The uncertainty principle does not just apply to position and momentum. In its general form, it applies to every pair of conjugate variables. An example of a pair of conjugate variables is the x-component of angular momentum (spin) vs. the y-component of angular momentum. In general, and unlike the case of position versus momentum discussed above, the lower bound for the product of the uncertainties of two conjugate variables depends on the system state.
Expression of finite available amount of Fisher information
The uncertainty principle alternatively derives as an expression of the Cramér-Rao inequality of classical measurement theory. This is in the case where a particle position is measured. See Stam (1959). The mean-squared particle momentum enters as the Fisher information in the inequality. See also extreme physical information.
Common observables which obey the uncertainty principle
To find uncertainty relations between physical observables, locate pairs of observables A and B whose commutator has certain analytic properties.
- The most common one is the uncertainty relation between position and momentum of a particle in space:
- The uncertainty relation between two orthogonal components of the total angular momentum operator of a particle is as follows:
-
- where i, j, k are distinct and Ji denotes angular momentum along the xi axis.
- The following uncertainty relation between energy and time is often presented in physics textbooks, although its interpretation requires more care because there is no operator representing time:
- For time and frequency pair, the relation is stated as:
The theorem
The uncertainty principle becomes a theorem in the theory of operators.
Theorem. For arbitrary symmetric operators A: H → H and B: H → H, and any element x of H such that A B x and B A x are both defined (so that in particular, A x and B x are also defined), then
This is an immediate consequence of the Cauchy-Bunyakovski-Schwarz inequality.
Consequently, the following general form of the uncertainty principle, first pointed out in 1930 by Howard Percy Robertson and (independently) by Erwin Schrödinger, holds:
This inequality is called the Robertson-Schrödinger relation.
The operator A B - B A is called the commutator of A, B and is denoted [A, B]. It is defined on those x for which A B x and B A x are both defined.
From the Robertson-Schrödinger relation, the following Heisenberg uncertainty relation is immediate:
Suppose A and B are two observables which are identified to self-adjoint (and in particular symmetric) operators. If B A ψ and A B ψ are defined then
where
is the operator mean of observable X in the system state ψ and
is the operator standard deviation of observable X in the system state ψ
The above definitions of mean and standard deviation are defined formally in purely operator-theoretic terms. The statement becomes more meaningful however, once we note that these actually are the mean and standard deviation for the measured distribution of values. See quantum statistical mechanics.
It may be evaluated not only for pairs of conjugate operators (e.g. those defining measurements of distance and of momentum, or of duration and of energy) but generally for any pair of Hermitian operators. There is also an uncertainty relation between the field strength and the number of particles which is responsible for the phenomenon of virtual particles.
Note that it is possible to have two non-commuting self-adjoint operators A and B which share an eigenvector ψ in this case ψ represents a pure state which is simultaneously measurable for A and B.
Generalizations
Other forms of the uncertainty principle can be formulated for the Fourier transform on general locally compact groups or for Fourier integral operators on manifolds. For example, Hirschman proved in 1957 a form of the uncertainty principle which is stronger than the Weyl form stated above.
History and interpretations of the principle
Main article: Interpretation of quantum mechanics
Albert Einstein was not happy with the uncertainty principle, and he challenged Niels Bohr and Werner Heisenberg with a famous thought experiment (See the Bohr-Einstein debates for more details): we fill a box with a radioactive material which randomly emits radiation. The box has a shutter, which is opened and immediately thereafter shut by a clock at a precise time, thereby allowing some radiation to escape. So the time is already known with precision. We still want to measure the conjugate variable energy precisely. Einstein proposed doing this by weighing the box before and after. The equivalence between mass and energy from special relativity will allow you to determine precisely how much energy was left in the box. Bohr countered as follows: should energy leave, then the now lighter box will rise slightly on the scale. That changes the position of the clock. Thus the clock deviates from our stationary reference frame, and again by special relativity, its measurement of time will be different from ours, leading to some unavoidable margin of error. In fact, a detailed analysis shows that the imprecision is correctly given by Heisenberg's relation.
Within the widely but not universally accepted Copenhagen interpretation of quantum mechanics, the uncertainty principle is taken to mean that on an elementary level, the physical universe does not exist in a deterministic form—but rather as a collection of probabilities, or potentials. For example, the pattern (probability distribution) produced by millions of photons passing through a diffraction slit can be calculated using quantum mechanics, but the exact path of each photon cannot be predicted by any known method. The Copenhagen interpretation holds that it cannot be predicted by any method.
It is this interpretation that Einstein was questioning when he said "I cannot believe that God would choose to play dice with the universe." Bohr, who was one of the authors of the Copenhagen interpretation responded, "Einstein, don't tell God what to do."
Einstein was convinced that this interpretation was in error. His reasoning was that all previously known probability distributions arose from deterministic events. The distribution of a flipped coin or a rolled dice can be described with a probability distribution (50% heads, 50% tails). But this does not mean that their physical motions are unpredictable. Ordinary mechanics can be used to calculate exactly how each coin will land, if the forces acting on it are known. And the heads/tails distribution will still line up with the probability distribution (given random initial forces).
Einstein assumed that there are similar hidden variables in quantum mechanics which underlie the observed probabilities.
Neither Einstein nor anyone since has been able to construct a satisfying hidden variable theory, and the Bell inequality illustrates some very thorny issues in trying to do so. Although the behavior of an individual particle is random, it is also correlated with the behavior of other particles. Therefore, if the uncertainty principle is the result of some deterministic process, it must be the case that particles at great distances instantly transmit information to each other to ensure that the correlations in behavior between particles occur.
The uncertainty principle in popular culture
The uncertainty principle is stated in popular culture in many ways, for example by stating that it is impossible to know both where an electron is and where it is going at the same time. This is roughly correct, although it fails to mention an important part of the Heisenberg principle, which is the quantitative bounds on the uncertainties. One common incorrect formulation is that observation of an event changes the event. This may be true in some cases for some events, but it has nothing to do with the uncertainty principle in quantum mechanics.
In some science fiction stories, a device to circumvent the uncertainty principle is called a Heisenberg compensator, most famously in Star Trek for use on the transporter; however, it is not clear what circumventing means.
In Stephen Donaldson's Gap Cycle science fiction book series, one of the characters postulates a socio-political version of the uncertainty principle: namely, that by determining his precise "location" in the current political landscape, he is prevented from simultaneously calculating the likely direction of political events in the near future.
Humor
The unusual nature of Heisenberg's uncertainty principle, and its distinctive name, has made it the source of several jokes. It is said that a popular item of graffiti at the physics department of university campuses is the slogan "Heisenberg may have been here."
In another uncertainty principle joke, a quantum physicist is stopped on the highway by a police officer who asks "Do you know how fast you were going, sir?", to which the physicist responds, "No, but I know exactly where I am!".
In the show Futurama there is a close finish in a horse race, a "quantum finish" they say, and a photograph reveals who won, when the professor yells out "No fair! You changed the outcome by measuring it!"
See also
References
Textbooks
- Griffiths, David J. (2004) Introduction to Quantum Mechanics (2nd ed.), Prentice Hall. ISBN 013805326X
- Omnes, Roland (1999) Understanding Quantum Mechanics, Princeton University Press. ISBN 0691004358
- J. von Neumann, Mathematical Foundations of Quantum Mechanics, Princeton University Press, 1955.
- H. Weyl, The Theory of Groups and Quantum Mechanics, Dover Publications 1950.
Journal articles
- G. Folland and A. Sitaram, The Uncertainty Principle: A Mathematical Survey, Journal of Fourier Analysis and Applications, 1997 pp 207-238.
- W. Heisenberg, Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Zeitschrift für Physik, 43 1927, pp 172-198. English translation: J. A. Wheeler and H. Zurek, Quantum Theory and Measurement Princeton Univ. Press, 1983, pp. 62-84.
- I Hirschman, A Note on Entropy, American Journal of Mathematics, 1957.
- A. J. Stam, Information and Control, vol. 2, 1959, p. 101.
External links
- aip.org: Quantum mechanics 1925-1927 - The uncertainty principle
- Eric Weisstein's World of Physics - Uncertainty principle
- John Baez on the time-energy uncertainty relation
- Schrödinger equation from an exact uncertainty principle
- Beating the uncertainty principle in finite-parameter systems
- Stanford Encyclopedia of Philosophy entry
- D. A. Arbatsky, The certainty principle
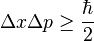


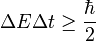
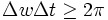
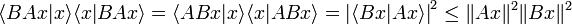
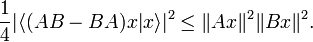
![\Delta_{\psi} A \, \Delta_{\psi} B \ge \frac{1}{2} \left|\left\langle\left[{A},{B}\right]\right\rangle_\psi\right|](http://en.wikipedia.org/math/1/d/3/1d3f2c1271a50c638f3e2bccd2e72ff4.png)



